Парная и множественная корреляция

При сравнении расчетного значения dw статистики с табличным:

- ряд остатков не коррелирован.

. Осуществим оценку надежности уравнения регрессии с помощью F-критерия Фишера:

.

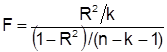Значение F-критерия Фишера можно найти с помощью инструмента Регрессия (Анализ данных в Excel): (табл. 2.7).

Таблица 2.7 - Дисперсионный анализ

Табличное значение F-критерия можно найти с помощью функции FРАСПОБР: при доверительной вероятности 0,95 при и составляет 4,737.

Поскольку , уравнение регрессии следует признать адекватным.

. Оценим с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии:

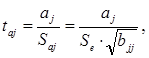
где - коэффициенты в матрице .

Воспользуемся инструментом Регрессия (Анализ данных в Excel (табл. 2.4):

.

Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР; при уровне значимости 5% и степенях свободы составляет 2,365.

Т.к. для двух коэффициентов, то коэффициенты и существенны (значимы).

. Построим точечный и интервальный прогнозы результирующего показателя.

Прогнозные значения Х1,11, Х2,11 можно определить с помощью методов экспертных оценок, с помощью средних абсолютных приростов или вычислить на основе экстраполяционных методов.

В качестве аппроксимирующей функции выберем полином второй степени (парабола), по которой построим прогноз на один шаг вперед.

Уравнение фактора - Среднегодовая ставка по кредитам:

и прогнозное значение .

Уравнение для Размера внутрибанковских расходов выглядит следующим образом:

.

Подставляя в него вместо , получим прогнозное значение среднегодовой ставки по кредитам .

Отобразим результаты расчетов на графике (рис.2.2; рис. 2.3).

Для получения прогнозных оценок зависимостей переменной по модели

Подставим в нее найденные прогнозные значения факторов Х1 и Х2.

.

Доверительный интервал прогноза будет иметь следующие границы: