Расчет эконометрических параметров
Задание 1
По приведенным данным требуется:
Построить модель парной регрессии y от x:
|
Номер района |
Средние выплаты социального характера на одного неработающего тыс. руб., y |
Прожиточный минимум в среднем на душу населения, тыс. руб.,x |
|
1 |
1077 |
481,5 |
|
2 |
1246 |
539,5 |
|
3 |
906 |
422,5 |
|
4 |
610 |
376,5 |
|
5 |
838 |
396,5 |
|
6 |
335 |
316,5 |
|
7 |
1470 |
652,5 |
|
8 |
450 |
343,5 |
|
9 |
1399 |
586,5 |
|
10 |
1213 |
755,5 |
|
11 |
1304 |
502,5 |
|
12 |
1343 |
713,5 |
|
13 |
1279 |
746,5 |
|
14 |
510 |
326,5 |
|
15 |
1163 |
762,5 |
Серия Г: линейную и параболическую (
).
Значение параметра с найдите подбором, используя пакет Еxcel. Критерий эффективности - наименьшее значение средней по модулю ошибки аппроксимации.
Рассчитать индекс парной корреляции (для линейной модели - коэффициент корреляции), коэффициент детерминации и среднюю по модулю ошибку аппроксимации.
Оценить каждую модель, применив критерий Фишера.
Линейную модель оценить с помощью t-критерия Стьюдента, найти доверительные интервалы для коэффициентов регрессии и корреляции (доверительная вероятность 0,95).
Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 30% от его среднего уровня. Для линейной модели с вероятностью 0,95 построить доверительный интервал для прогнозного значения результата.
Составить сводную таблицу результатов вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
Результаты расчетов отобразить на графиках.
Построим линейную модель парной регрессии у = а * х + b, вспомогательные расчеты проводим в таблице (стр. 8)
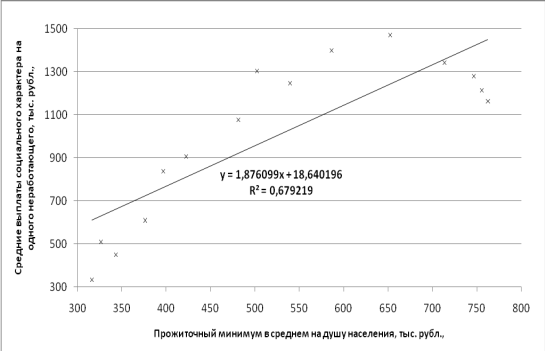
Найдём средние значения прожиточного минимуму х и соц. выплат у:
;
.
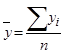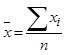Затем для каждого i-го года вычислим отклонения: 
и 
, 
, а затем перемножим эти отклонения и найдём среднее арифметическое полученной величины, т.е. определим выборочную ковариацию
